DETERMINAN MATRIKS

KATA MAHASISWA

Cara Determinan Matriks

Salah satu bagian paling penting dari pembahasan materi matriks adalah cara menghitung determinan matriks, invers matriks, dan sifat-sifatnya. Sobat idschool perlu meneguasai dasar cara menentukan determinan matriks, invers matriks, dan sifat-sifatnya karena akan sangat dibutuhkan untuk membantu perhitungan matriks dengan tipe soal tingkat lanjut. Namun sebelumnya, sebaiknya sobat idschool sudah menguasai bagaimana cara mengoperasikan dua matriks atau lebih.

Untuk pertama, sobat idschool akan dikenalkan melalui bagian yang paling sederhana yaitu mencari determinan matriks dengan ordo 2 x 2. Untuk tingkat SMA, ulasan mengenai determinan matriks biasanya melibatkan matriks dengan ordo 2 x 2. Namun, materi determinan matriks dengan ukuran lebih besar juga sering diulas. Hanya saja tidak sesering determinan matriks ordo 2 x 2. Cara menentukan determinan matriks untuk orde lebih besar dari 3 x 3 lebih rumit dari cara menentukan determinan matriks ordo 2 x 2.

Menentukan nilai invers matriks ordo 2 x 2 cukup mudah dilakukan. Sedangkan cara menentukan invers matriks ordo 3 x 3 lebih susah dan rumit. Melalui halaman ini, sobat idschool bisa menyimak cara menentukan invers matriks dari kedua ordo tersebut.

Uraian materi yang dibahas pada halaman ini memuat apa itu determinan matriks dan bagaimana cara menentukan determinan matriks? Apa itu invers matriks dan bagaimana cara menghitung nilai invers matriks? Sifat apa saja yang dimiliki determinan matriks dan invers matriks?

Secara lebih lengkap dapat disimak pada pembahasan di bawah.

• Determinan

Dalam bidang aljabar linear, determinan adalah nilai yang dapat dihitung dari unsur suatu matriks persegi. Determinan matriks A ditulis dengan tanda det(A), det A, atau |A|. Determinan dapat dianggap sebagai faktor penskalaan transformasi yang digambarkan oleh matriks.

Apabila matriksnya berbentuk 2 × 2, rumus untuk mencari determinan adalah:

${\displaystyle {\begin{aligned}|A|={\begin{vmatrix}a&b\\c&d\end{vmatrix}}=ad-bc.\end{aligned}}}$

Apabila matriksnya berbentuk 3 × 3 matrix A, rumusnya adalah:

${\displaystyle {\begin{aligned}|A|={\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}&=a\,{\begin{vmatrix}e&f\\h&i\end{vmatrix}}-b\,{\begin{vmatrix}d&f\\g&i\end{vmatrix}}+c\,{\begin{vmatrix}d&e\\g&h\end{vmatrix}}\\&=aei+bfg+cdh-ceg-bdi-afh.\end{aligned}}}$

Cara menghitung determinan pada matriks dengan ordo tiga biasa disebut dengan Aturan Sarrus. Untuk lebih jelasnya, lihat penjelasan pada gambar di bawah.

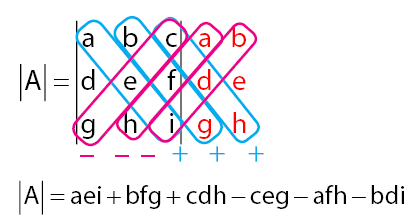
Contoh perhitungan determinan pada matriks ordo 3:

  

Maka,

  

  

  

  

Rumus Leibniz untuk mencari determinan matriks n × n adalah:

${\displaystyle \det(A)=\sum _{\sigma \in S_{n}}\left(\operatorname {sgn}(\sigma )\prod _{i=1}^{n}a_{i,\sigma _{i}}\right).}$

Metode eliminasi Gauss juga dapat dipakai. Sebagai contoh, determinan matriks berikut:

${\displaystyle A={\begin{bmatrix}-2&2&-3\\-1&1&3\\2&0&-1\end{bmatrix}}}$

dapat dihitung dengan menggunakan matriks berikut:

${\displaystyle B={\begin{bmatrix}-2&2&-3\\0&0&4.5\\2&0&-1\end{bmatrix}},\quad C={\begin{bmatrix}-2&2&-3\\0&0&4.5\\0&2&-4\end{bmatrix}},\quad D={\begin{bmatrix}-2&2&-3\\0&2&-4\\0&0&4.5\end{bmatrix}}.}$

Di sini, B diperoleh dari A dengan menambahkan −1/2× baris pertama dengan baris kedua, sehingga det(A) = det(B). C diperoleh dari B dengan menambahkan kolom pertama dengan kolom ketiga, sehingga det(C) = det(B). Sementara itu, D didapat dari C dengan menukar kolom kedua dan ketiga, sehingga det(D) = −det(C). Determinan matriks segitiga D merupakan hasil dari perkalian diagonal utamanya: (−2) · 2 · 4.5 = −18. Maka dari itu, det(A) = −det(D) = +18.